About Me

- Ravi Bhide
- Ravi is an armchair futurist and an aspiring mad scientist. His mission is to create simplicity out of complexity and order out of chaos.
Monday, March 12, 2012
Friday, February 10, 2012
Randomized Rounding for Integer Programming
Motivation
- Solving equations that allow just integer solutions is usually harder than solving for fractions. An example is the knapsack problem, whose fractional form can be solved in linear time, but its integer form is NP-complete.
- An intuitive way to reduce the computational complexity of integer programming is to approximate the integer solution by the following process:
- Solve the fractional problem instead.
- Round off fractions to integers "intelligently" and
- Know the bounds on error or non-optimality introduced by this approximation.
- In this article, we round off fractions randomly (based on some probability), hence the name.
Introduction
This article is motivated by the "Wiring Problem" as discussed in the book Randomized Algorithms by Motwani and Raghavan. This problem can be stated as follows:
Given a grid of squares, lay out wires between the given squares. Number of wires crossing any boundary of any square is to be constrained to no more than a given number $\omega_0$. Furthermore, minimize the maximum number of wires that cross any boundary.
Refer to the diagram below that shows a 3x3 grid, with 3 wires (labeled in red). For clarity, boundaries are labeled in blue separately. Each row has 2 vertical and 3 horizontal boundaries, for a total of 12 for the grid.
We limit ourselves to solutions containing a maximum of one "turn" in the wire. In the above diagram, wires 1 and 2 have one turn in them, while wire 3 has no turns ("it is straight").
Solving this problem involves solving the integer programming problem, which is NP-complete. Instead, we will solve it using randomization, which reduces the complexity significantly (down to the complexity of solving the fractional linear programming problem). Given below is a mathematical analysis of this solution.
Notation
- We number wires from $1$ to $a$. So, in the above diagram, we have $a=3$. We use the subscript $i$ for wires.
- For each wire $i$, we have 2 variables - $h_i$ and $v_i$ denoting whether the first part of the wire is horizontal or vertical.
- If the first part is horizontal, then $h_i=1$ and $v_i=0$.
- If the first part is vertical, then $h_i=0$ and $v_i=1$.
- So, for all wires $h_i,v_i\in\{0,1\}$
- In the above wiring, {$h_1=0$, $v_1=1$}, {$h_2=1$, $v_2=0$} and {$h_3=0$, $v_3=1$}.
- Additionally, this means that only one of $h_i$ and $v_i$ is 1 and the other is 0, since the first part of any wire can either be horizontal or vertical (at least one) and not both. So, for all wires: \[h_i+v_i=1\]
- We number boundaries from $1$ to $b$. So, in the above diagram, we have $b=12$. We use the subscript $j$ for boundaries.
- For each boundary $j$, we have 2 variables - $H_j$ and $V_j$ - denoting the wires that pass through that boundary.
- $H_j$ is the set of all wires that start out horizontally and pass through boundary $j$.
- Analogously, $V_j$ is the set of all wires that start out vertically and pass through boundary $j$.
- As examples, {$H_3=1$, $V_3=0$}, {$H_7=0$, $V_7=1$}. It is important to note that {$H_9=1$, $V_9=1$}, since the number of wires that start out horizontally and pass through boundary 9 is 1 (wire 2)
- Let $F_j$ denote the number of wires passing through boundary $j$. Since that number is no more than $\omega_0$: \[F_j=\sum_{i\in{H_j}}{h_i}+\sum_{i\in{V_j}}{v_i}\leq\omega_0\]
- The first summand corresponds to the number of wires that start out horizontally and pass through boundary $j$.
- The second summand corresponds to those that start out vertically and pass through boundary $j$.
- Their sum, which denotes the total number of wires passing through boundary $j$, obviously has to be no more than the specified constraint, $\omega_0$.
- Note that $F_j$ is an objective function in the linear programming terminology.
- Let $F=\max{F_j}$, i.e. the maximum number of wires passing through any boundary with a given solution. The solution with the least $F$ value is the optimal solution. In other words, the solution that requires the lowest maximum of wires passing through any boundary is defined as the optimal solution.
Randomized Rounding
- We first solve the linear programming problem using fractional values. There are well-known algorithms that solve this problem in polynomial time.
- Let $\widehat{h_i}$ and $\widehat{v_i}$ denote the fractional value solutions (e.g. 0.65 and 0.35, they are constrained to add up to 1). Note that they are the fractional counterparts to integer solutions, $h_i$ and $v_i$ (e.g. 1 and 0). So we have \[\widehat{F_j}=\sum_{i\in{H_j}}\widehat{h_i}+\sum_{i\in{V_j}}\widehat{v_i}\leq\widehat{\omega}\leq\omega_0\] where $\widehat{F_j}$ is the number of wires crossing boundary $j$ in the fractional case (so this will be a fraction, generally, e.g. $2.8$).
- The reason $\widehat{\omega}\leq\omega_0$ is that the fractional solution $\widehat{\omega}$ could potentially be "more optimal" (because it is not constrained by integer values) and hence lower than $\omega_0$.
- Since $h_i$ and $v_i$ denote how wire $i$ is to be oriented, $\widehat{h_i}$ and $\widehat{v_i}$ can be considered as approximations (in fact, probabilities) to this orientation.
- Here comes the crux of the randomized rounding approach. We round off $\widehat{h_i}$ to 1 with probability $\widehat{h_i}$ and to 0 with the remaining probability. E.g. if the fractional linear programming solution has $\widehat{h_i}=0.65$ and consequently, $\widehat{v_i}=0.35$, then we round off $\widehat{h_i}$ to 1 with probability 0.65 and to 0 with probability 0.35.
- Lets call the rounded off variable as $\overline{h_i}$ and $\overline{v_i}$ respectively. Note that these are random variables and not values. That means, probability $\mathbf{P}(\overline{h_i}=1)=\widehat{h_i}$ and $\mathbf{P}(\overline{h_i}=0)=1-\widehat{h_i}$. Note that mean of this variable, $\mathbf{E}(\overline{h_i})=\widehat{h_i}$.
- What can we say about the value of the objective function for these random variables (which denotes the number of wires crossing boundary $j$ in the randomized scenario)? In other words, what can we say about the random variables \[\overline{F_j}=\sum_{i\in{H_j}}\overline{h_i}+\sum_{i\in{V_j}}\overline{v_i}\]
- We derive the expected value (mean) of these random variables. \[\mathbf{E}(\overline{F_j})=\mathbf{E}(\sum_{i\in{H_j}}\overline{h_i}+\sum_{i\in{V_j}}\overline{v_i})\] By linearity of expecations, we have \[=\mathbf{E}(\sum_{i\in{H_j}}\overline{h_i})+\mathbf{E}(\sum_{i\in{V_j}}\overline{v_i})\] \[=\sum_{i\in{H_j}}\mathbf{E}(\overline{h_i})+\sum_{i\in{V_j}}\mathbf{E}(\overline{v_i})\] \[=\sum_{i\in{H_j}}\widehat{h_i}+\sum_{i\in{V_j}}\widehat{v_i}\[\leq\widehat\omega\hspace{4mm}\text{(from (1))}\]
- In other words, $\mathbf{E}(\widehat{F_j})\leq\widehat{\omega}\hspace{2mm}\forall{j}$. This means that the mean value of each of the objective functions $\widehat{F_j}$ is bounded from above by $\widehat\omega$ (which, by the way, happens to be better than our original bound of $\omega_0$ (from (1)).
- This means that, on an average, the number of wires crossing a boundary in the randomized scenario is equal to the value in the fractional scenario, for each boundary. This is huge, since that value is better than the value in the integer scenario!
Probabilistic analysis
- Let $\omega_S$ be the maximum number of wires passing through any boundary in our solution $S$ obtained from the above randomized rounding algorithm.
- We would like to determine how far this $\omega_S$ deviates from either our optimal solution $\omega_0$ for integer values or $\widehat{\omega}$ for fractional values.
- Graphically, in the diagram below, we are trying to find out how far $\omega_S$ is from $\widehat{\omega}$ or $\omega_0$, if we are willing to tolerate a maximum error of $\epsilon$.
- If the grid has $n$ squares, we have no more than $2n$ boundaries. This implies that for each boundary, we can tolerate an error of no more than $\epsilon/2n$.
- Chernoff bound gives us the following: \[\mathbf{P}[X\geq(1+\delta)\mu]<\left\{\frac{e^\delta}{(1+\delta)^{(1+\delta)}}\right\}^\mu=\epsilon/2n\] where $\mu$ is the mean and $\delta$ is the relative distance away from the mean.
- In our case, $\mu=\widehat{\omega}$ and we would like to find the value of $\delta$ such that the error is $\epsilon$. The exact value of $\delta$ that gives a specified error of $\epsilon/2n$ is quite complicated to determine and we will denote it as $\Delta^{+}(\mu,\epsilon/2n)$.
- Substituting this value in the Chernoff bound equation, we get \[\omega_S<\widehat{\omega}(1+\Delta^{+}(\mu,\epsilon/2n))\]
- While $\Delta^{+}(\mu,\epsilon/2n)$ is hard to determine, it is usually quite small, $O(1/n)$.
- This means that as the number of squares in the grid increases, the solution given by the randomized case increasingly approximates the solution given by the fractional case! In other words, the orientation of each wire determined by the randomized case is increasingly the optimal orientation, as the size of the grid increases.
We took an integer programming problem (which is NP-complete), solved it using fractional linear programming (which is polynomial time), used randomization to approximate each fraction to its integer
equivalent and found that for large grids, the solution that this approximation yields is fairly close to the optimal solution for the original, integer programming problem.
References
- Motwani, R. and Raghavan, P., Randomized Algorithms, 2007.
Saturday, December 24, 2011
Stable Marriage Problem
Java-based implementation of the Gale-Shapley algorithm to solve the stable marriage problem can be found here: github/rbhide0/pudding.
Labels:
gale-shapley,
randomized,
solution,
stable marriage
Friday, December 16, 2011
Randomized two point sampling
While reading "Randomized Algorithms" by Motwani and Raghavan, I felt that the authors' treatment of the topic of "two point sampling" was a little too short and summarized. In this article, I provide some details around this topic.
Motivation
When using randomized algorithms, for a given input $x$, the usual strategy is to choose $n$ random numbers (a.k.a. "witnesses") and run a deterministic algorithm on the input using each of the random numbers. The intuition is that if the deterministic algorithm has a probability of error $\epsilon$ (e.g. $1/3$), $n$ independent runs reduce this probability to $\epsilon^n$ (e.g. $1/3^n$).
The above assumes that we have the option to choose $n$ independent random numbers. What happens if that option were constrained to choosing no more than a constant $c$ random numbers? We look at the simple case where we choose just 2 random numbers ($c=2$), giving it the name two-point. So, the main question we are trying to answer is the following:
The idea is to generate $n$ numbers based on the chosen 2 random numbers and use them in lieu of the $n$ purely independent random numbers. These generated numbers are dependent on the 2 chosen numbers. Hence they are not independent, but are pairwise independent. This loss of full independence reduces the accuracy of the algorithmic process, but it is still quite usable.
The Process
Motivation
When using randomized algorithms, for a given input $x$, the usual strategy is to choose $n$ random numbers (a.k.a. "witnesses") and run a deterministic algorithm on the input using each of the random numbers. The intuition is that if the deterministic algorithm has a probability of error $\epsilon$ (e.g. $1/3$), $n$ independent runs reduce this probability to $\epsilon^n$ (e.g. $1/3^n$).
The above assumes that we have the option to choose $n$ independent random numbers. What happens if that option were constrained to choosing no more than a constant $c$ random numbers? We look at the simple case where we choose just 2 random numbers ($c=2$), giving it the name two-point. So, the main question we are trying to answer is the following:
If our randomized algorithm reduced the probability of error to $\epsilon^n$ with $n$ random numbers, what can we expect about the probability of error with $2$ randoms? $\epsilon^2$ is an obvious bound, but can we do any better? It turns out that we can indeed do better and reduce the probability of error to $1/n$. This is significantly better than the constant, $\epsilon^2$.The High-level Idea
The idea is to generate $n$ numbers based on the chosen 2 random numbers and use them in lieu of the $n$ purely independent random numbers. These generated numbers are dependent on the 2 chosen numbers. Hence they are not independent, but are pairwise independent. This loss of full independence reduces the accuracy of the algorithmic process, but it is still quite usable.
The Process
- Choose a large prime number, $\rho$ (e.g. Mersenne prime, $2^{31}-1$).
- Define $\mathbb{Z}_\rho$ as the ring of integers modulo $\rho$. (e.g. $0,1,\cdots,2^{31}-2$)
- Choose 2 random numbers, $a$ and $b$ from $\mathbb{Z}_\rho$. (e.g. $a=2^{20}+781$ and $b=2^{27}-44$). These are the only independent random numbers that are picked for two-point sampling.
- Generate $n$ "pseudo-random" numbers $y_i=(a*i+b)\mod{\rho}$. E.g.
- $y_0=2^{27}-44$
- $y_1=(2^{20}+781)*1+2^{27}-44$
- $y_2=(2^{20}+781)*2+2^{27}-44$ and so on.
- Use each of $y_i$s as witnesses in lieu of independent random witnesses, for algorithm $\mathbi{A}$.
Notation
- Let $\mathbi{A}(x,y)$ denote the output of the execution of a deterministic algorithm $\mathbi{A}$ on input $x$ with witness $y$. We restrict this algorithm to return only $1$ or $0$. If the algorithm outputs $1$, we can be sure that $1$ is the right answer. If the algorithm outputs $0$, the right answer could be either $1$ or $0$.
- $\mathbi{A}(x,y)$ produces correct output (which could be either $1$ or $0$) with probability $p$, meaning it produces a possibly erroneous output (i.e. a $0$ instead of $1$) with probability $1-p$.
- Let $Y_i=\mathbi{A}(x,y_i)$ be a random variable, where $y_i$ is a psuedo-random number defined earlier. Note that the expected value of $Y_i$, $\mathbf{E}[Y_i]=p$, since $\mathbi{A}(x,y)$ produces a correct output with probability $p$.
- Let $Y=\sum{Y_i}$. By linearity of expectations, $\mathbf{E}[Y]=\mathbf{E}[\sum{Y_i}]=\sum{\mathbf{E}[Y_i]}=np$. Note that linearity of expectations is agnostic to the dependence between the random variables $Y_i$.
- Note that variance of $Y$, $\sigma^{2}_{Y}=np(1-p)$.
Derivation
We are trying to determine the error for the randomized process after $n$ runs of the deterministic algorithm $\mathbi{A}$. This is at most the probability of the event where each of the $n$ runs produced an erroneous output of $0$, i.e. each of $Y_i=0$, or equivalently, $Y=0$. (Note that some outputs of $0$ are not erroneous, hence the use of the words "at most".) So we are trying to determine $\mathbf{P}[Y=0]$.
Since $Y_i$s are not all independent, we cannot say:
\[\mathbf{P}[Y=0]=\prod{\mathbf{P}[Y_i=0]}\leq(1-p)^{n}\]
So, alternatively, we would like to know:
\[\mathbf{P}[|Y-\mathbf{E}[Y]|\geq\mathbf{E}[Y]]\]
which, by Chebyshev's inequality is:
\[\leq(\sigma_{Y}/\mathbf{E}[Y])^2\]
\[=\frac{np(1-p)}{n^2p^2}\]
\[=\frac{1-p}{np}\]
\[=O(\frac{1}{n})\]
Intuitively, this means that for any given error bound $\epsilon$, instead of requiring $O(\log(1/\epsilon))$ runs of the deterministic algorithm $\mathbi{A}$ in the case of $n$ independent random witnesses, we will require $O(1/\epsilon)$ runs in the case $2$ independent random witnesses. This is exponentially larger. So, it is not as efficient, but it is not the end of the world either!
In Closing
The above derivation shows that two random numbers are sufficient to minimize the error of a randomized algorithm below any given bound, although this comes with loss of some efficiency.
References
- Motwani, R. and Raghavan, P., Randomized Algorithms, 2007.
Friday, November 11, 2011
Greedy algorithm for grid navigation
For navigation problems that can be modeled as a grid with obstacles, we present a greedy algorithm that can determine a navigable path between any two given points on the grid.
Grid properties
Grid properties
- Rectangular board of size $m$ by $n$, so it has $m*n$ squares
- A square can be navigable or blocked (e.g. an obstacle)
- A square $(i, j)$ has the following adjacent squares:
- $(i-1, j-1)$ - corresponds to the south-west direction
- $(i-1, j)$ - corresponds to the west direction
- $(i-1, j+1)$ - corresponds to the north-west direction
- $(i, j-1)$ - corresponds to the south direction
- $(i, j+1)$ - corresponds to the north direction
- $(i+1, j-1)$ - corresponds to south-east direction
- $(i+1, j)$ - corresponds to the east direction and
- $(i+1, j+1)$ - corresponds to the north-east direction
- From a given square, one can navigate to any of the adjacent squares, unless that square is blocked or is beyond the board margins.
The objective
Given 2 points on the board - the source $s$ and the destination $d$, find a navigable path between $s$ and $d$.
Navigation algorithm
- We use a vector $\overrightarrow{v}$ ("the destination vector") to determine the direction of our destination from our current position $p$. \[\overrightarrow{v}=\overrightarrow{d}-\overrightarrow{p}=(d_x-p_x,d_y-p_y)\]
- A direction vector is a vector of unit length in a direction. E.g. east direction vector $\overrightarrow{i_{1}}=(1,0)$, north-east =$\overrightarrow{i_{2}}=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$.
- We use vector dot product to determine the degree of alignment between the destination vector $\overrightarrow{v}$ and each of the direction vectors ($\overrightarrow{i_{1}},\cdots,\overrightarrow{i_{8}}$).
- The direction vector with the best possible alignment with the destination vector, i.e. the one with the largest dot product, is the direction we take. In other words, the direction corresponding to the largest of {$(\overrightarrow{v}\cdot\overrightarrow{i_{1}}),(\overrightarrow{v}\cdot\overrightarrow{i_{2}}),\cdots,(\overrightarrow{v}\cdot\overrightarrow{i_{8}})$} is our choice.
- If we have already visited the square corresponding to this direction, we choose the next best direction available based on the dot product.
- We repeat the above steps till we reach our destination (or a pre-determined upper bound on the path length, at which point we abort.)
Properties of the algorithm
- This is a greedy algorithm. It chooses the direction to navigate in, based only on the current square it is in.
- For a grid with low obstacle ratio (e.g. less than half the squares are obstacles), this algorithm converges to a navigable path fairly quickly - in about 2 times the global shortest path or less, discounting outliers.
Implementation
You can find java source code here - https://github.com/briangu/amaitjo/blob/master/src/main/java/ravi/contest/ants/movement/NavigationAdvisor.java
You can find java source code here - https://github.com/briangu/amaitjo/blob/master/src/main/java/ravi/contest/ants/movement/NavigationAdvisor.java
Tuesday, November 8, 2011
Markov and Chebyshev inequalities
Markov inequality
Intuitively, this inequality states that the probability that a random variable's value is much greater than its mean is low and that the larger this value, the smaller its probability. It states that \[\mathbf{P}(X\geq a)\leq\frac{\mu}{a},\hspace{10 mm}\forall a>0\] where $\mu$ is the mean, a.k.a. the expected value $\mathbf{E}(X)$ of the random variable. Note that this inequality needs that the random variable $X$ take non-negative values.
Here are some examples
Intuitively, this inequality states that the probability that a random variable's value is much greater than its mean is low and that the larger this value, the smaller its probability. It states that \[\mathbf{P}(X\geq a)\leq\frac{\mu}{a},\hspace{10 mm}\forall a>0\] where $\mu$ is the mean, a.k.a. the expected value $\mathbf{E}(X)$ of the random variable. Note that this inequality needs that the random variable $X$ take non-negative values.
Here are some examples
- $\mathbf{P}(X\geq 10)\leq\mu/10$, which doesn't say much since $\mu$ could be greater than $10$. But the next one is more interesting.
- $\mathbf{P}(X\geq10\mu)\leq1/10$, which means that the probability that a random variable is $10$ times its mean is less than or equal to $0.1$. Now that wasn't obvious before!
Chebyshev inequality
Unlike Markov inequality that involves just the mean, Chebyshev inequality involves the mean and the variance. Intuitively, it states that the probability of a random variable taking values far outside of its variance is low and the farther this value from its mean, the lower its probability. More formally, it states that \[\mathbf{P}(|X-\mu|\geq c)\leq\frac{\sigma^2}{c^2},\hspace{10 mm}\forall c>0\] This implies \[\mathbf{P}({X-\mu|\geq k\sigma)\leq\frac{1}{k^2}\] This means that the probability that a value falls beyond $k$ times the standard deviation is at most $1/k^2$. This inequality tends to give tighter bounds than Markov inequality.
More concretely
- $\mathbf{P}(|X-\mu|\geq2\sigma)\leq1/4$, which means that the probability that a random variable takes values outside of 2 times its standard deviation is less than $1/4$.
- $\mathbf{P}(|X-\mu|\geq3\sigma)\leq1/9$, which means that the probability that a random variable takes values outside of 3 times its standard deviation is less than $1/9$.
From Markov inequality to Chebyshev inequality
Derivation of Chebyshev inequality from Markov inequality is relatively straight forward. Let $Y=|X-\mu|^2$. According to Markov inequality \[\mathbf{P}(Y\geq c^2)\leq \mathbf{E}(Y)/c^2\] Since $\mathbf{E}(Y)=\sigma^2$ and $\mathbf{P}(Y\geq c^2)$ is equivalent to $\mathbf{P}(|X-\mu|\geq c)$, by substituting them, we get Chebyshev inequality \[\mathbf{P}(|X-\mu|\geq c)\leq\frac{\sigma^2}{c^2}\]
Sunday, August 14, 2011
Evaluating interviewers - Part 2
In this post, I show a method to mathematically evaluate an interviewer based on the job performance of the candidate that gets hired. This is a continuation of (but independent of) Evaluating Interviewers - Part 1, where I showed a method to evaluate an interviewer against other interviewers. I am replicating the definitions here from Part 1.
Definitions
What we expect from interview scores
We take the interviewer's score $s_{ij}$ as a prediction about the candidate $C_i$'s job performance once hired. The higher the score, the better the predicted job performance. E.g., when an interviewer gives a score of $3.1$ to candidate $C_1$ and $3.2$ to $C_2$, in effect, he is vouching for candidate $C_2$ to out-perform candidate $C_1$, by a margin proportional to $0.1$.
Secondly, we expect job performance to be directly and linearly proportional to the score. E.g., if scores of $3.1$ and $3.2$ translate to job performance ratings of $3.1$ and $3.2$ respectively, then a score of $3.3$ should translate to a job performance rating of $3.3$ or thereabouts.
In other words, we expect the following from our scores:
Good interviewer v/s Bad interviewer
We classify an interviewer as good when there is high correlation between the score given by the interviewer to the candidate and the job performance of the candidate post-hire. The higher the correlation, i.e. the lower the variance, the better the interviewer. This is because a lower variance implies better predictability on part of the interviewer. Conversely, the higher the variance, the worse the interviewer.
Here is a graph of job performance (Y-axis) against interviewer score (X-axis) for a good interviewer:
Here is the graph for a bad interviewer. Notice the high variance, implying a low correlation between interview score and job performance:
Easy v/s Hard interviewers
Variation from $y=x$ line doesn't necessarily indicate a bad interviewer. For an interviewer to be bad, the correlation between interview score and job performance should be low.
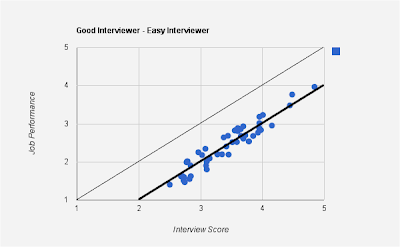
Here is an example of a good interviewer with high correlation between interview score and job performance, but whose mean is different from $y=x$ line.
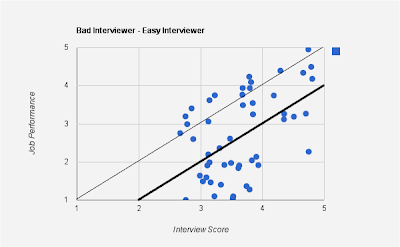
As opposed to the good interviewers, here are graphs for bad interviewers.
In the above case, the interviewer is an easy interviewer - one who tends to give a higher scores than his peers, as seen from the mean line (thicker one parallel to $y=x$ line). However, the low correlation suggests that the interviewer's score does not accurately portray job performance.
Here is another bad interviewer - this time a hard one - one who tends to give lower scores than his peers.
Definitions
| Symbol | Definition |
| $C_i$ | $i^{th}$ candidate |
| $R_j$ | $j^{th}$ interviewer |
| $s_{ij}$ | score for the $i^{th}$ candidate by the $j^{th}$ interviewer (this is the grade, usually between 1 and 5, given by the interviewer to the candidate based on the interview) |
| $m_i$ | number of interviewers in the interview panel for candidate $i$ (the number of interviewers, usually between 4 and 8, that the candidate faces during the course of the interview process) |
| $n_j$ | number of candidates interviewed by interviewer $j$ (can be large, in tens or hundreds, especially for popular interviewers) |
| $\hat{n_j}$ | number of candidates interviewed by interviewer $j$ that joined the company/group |
| $p_i$ | job performance of $i^{th}$ candidate after joining the company/group (usually between 1 and 5, captured in a company-internal HRM system) |
| $s_i$ | average score given by the interview panel for the $i^{th}$ candidate, $s_i=\sum_{j}s_{ij}/{m_i}$ (usually between 1 and 5) |
What we expect from interview scores
We take the interviewer's score $s_{ij}$ as a prediction about the candidate $C_i$'s job performance once hired. The higher the score, the better the predicted job performance. E.g., when an interviewer gives a score of $3.1$ to candidate $C_1$ and $3.2$ to $C_2$, in effect, he is vouching for candidate $C_2$ to out-perform candidate $C_1$, by a margin proportional to $0.1$.
Secondly, we expect job performance to be directly and linearly proportional to the score. E.g., if scores of $3.1$ and $3.2$ translate to job performance ratings of $3.1$ and $3.2$ respectively, then a score of $3.3$ should translate to a job performance rating of $3.3$ or thereabouts.
In other words, we expect the following from our scores:
So we expect a plot of job performance (Y-axis) against interview score (X-axis) to be roughly linear for each interviewer, ideally along the $y=x$ line. We will discuss variations from this line and its implications later in the article.
- Ordinality: if $s_{aj}>s_{bj}$, then we hold interviewer $R_j$ to a prediction that candidate $C_a$ would outperform $C_b$ on the job.
- Linearity: job performance should be directly and linearly proportional to the score.
Good interviewer v/s Bad interviewer
We classify an interviewer as good when there is high correlation between the score given by the interviewer to the candidate and the job performance of the candidate post-hire. The higher the correlation, i.e. the lower the variance, the better the interviewer. This is because a lower variance implies better predictability on part of the interviewer. Conversely, the higher the variance, the worse the interviewer.
Here is a graph of job performance (Y-axis) against interviewer score (X-axis) for a good interviewer:
Here is the graph for a bad interviewer. Notice the high variance, implying a low correlation between interview score and job performance:
Easy v/s Hard interviewers
Variation from $y=x$ line doesn't necessarily indicate a bad interviewer. For an interviewer to be bad, the correlation between interview score and job performance should be low.
Here is an example of a good interviewer with high correlation between interview score and job performance, but whose mean is different from $y=x$ line.
Note that the above graph satisfies both the ordinality and linearity conditions and hence the interviewer is a good interviewer. The above graph is for an "easy" interviewer - one who tends to give a higher score than those of his peers. Notice that the mean line hangs below the $y=x$ line.
Here is another example of an interviewer with high correlation between interview score and job performance, but whose mean is different from $y=x$ line.
This is a "hard" interviewer - one who tends to give a lower score than those of his peers. Notice that the mean line hangs above the $y=x$ line.
As opposed to the good interviewers, here are graphs for bad interviewers.
In the above case, the interviewer is an easy interviewer - one who tends to give a higher scores than his peers, as seen from the mean line (thicker one parallel to $y=x$ line). However, the low correlation suggests that the interviewer's score does not accurately portray job performance.
Here is another bad interviewer - this time a hard one - one who tends to give lower scores than his peers.
The above graphs show that both easy and hard interviewers can be good interviewers. And on the flip side, both easy and hard interviewers can be bad interviewers. What really distinguishes good from bad is how "tightly" the points hug the mean line in the graph. With this as the background, here is some math that will order interviewers in the descending order of "goodness".
The Math
- Find the line parallel to $y=x$ that serves as the mean for all points in the graph. There can be different definitions for "mean" here - e.g. one that is a mean of all $x$ and $y$ co-ordinates of the points, one that minimizes the sum of distances to each point, etc. For simplicity, we choose the mean of all $x$ and $y$ coordinates for that interviewer, i.e. $\overline{x}_j$ and $\overline{y}_j$ for interviewer $R_j$ respectively.
\[\overline{x}_j=\frac{\sum_{k}s_{kj}}{\hat{n_j}}\]
\[\overline{y}_j}=\frac{\sum_{k}p_k}{\hat{n_j}}\]
So the dark line in the graph corresponds to $y=f_j(x)=x+(\overline{y}_j-\overline{x}_j)$.
- We compute the standard deviation of interviewer $R_j$'s score, $\sigma_j$, as follows.
\[\sigma_j=\sqrt{\frac{\sum_k{(p_{i_k}-f_j(s_{i_kj}))^2}}{\hat{n_j}-1}}\]
where subscript $i_k$ is used to indicate a candidate that the interviewer interviewed and was eventually hired. So, essentially, we are determining the variance of the points with respect to the line $y=f_j(x)$. The lower the $\sigma_j$, the better the interviewer is at predicting the job performance of the candidate.
- Alternatively, instead of the above steps, we can compute the correlation coefficient between the interview scores and the job performance score.
- Order interviewers $R_j$ based on descending order of $\sigma_j$ (or the correlation coefficient). This is the list of interviewers - from the best to the worst - in that order!
In Closing
- We outlined one approach to rank interviewers according to their ability to predict future performance of a job candidate.
- There are many ways in which the "goodness" of an interviewer can be defined. Each can alter our algorithm.
- There are many ways in which one can define average performance of the interviewer (the dark solid line in the graph). We choose a simple definition.
- Regardless of the customization applied to our algorithm, the graphs and the rankings can help the organization better the interview process, thus:
- if an interviewer is deemed "bad", retrain them
- if an interviewer is deemed "easy", perhaps discount their score for the candidate by their variance, $\sigma_j$ to determine what a regular interviewer's score would have been for that candidate.
- similarly, for a "hard" interviewer, add their variance $\sigma_j$ to normalize their score and bring it up to par with other "regular" interviewers.
Subscribe to:
Posts (Atom)


.JPG)